江海志の博客

    登录
    最新消息：非无江海志，潇洒送日月

    最新发布 第2页

    江海志の博客: 记录学习生活的点点滴滴

    电子设备

    MacOS下让Adobe Creative Cloud等应用不再开机自启动

    江海志 6年前 (2018-11-11) 16488浏览 1评论

    弄了个PS安到系统，Adobe挺讲究，免费赠送安装了Adobe Creative Cloud等程序，启动系统时会跟上一堆Adobe的各种服务，就差全家捅了。看着碍眼，不用时也站系统资源。网上看了一些去除Adobe自启动的方法，有点不甘心，有那么费劲吗？算了来干货： 以下操作我假装用终端，这样显得逼格高一些： 一、 查看开机启动的应用：   cd /Library...

    基于浏览器隐藏www子域名的攻击与子域名泛解析劫持攻击
    网络安全

    基于浏览器隐藏www子域名的攻击与子域名泛解析劫持攻击

    江海志 6年前 (2018-09-17) 466410浏览 1评论

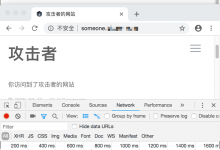
    Chrome 决定在版本70中隐藏地址栏里的www域名头部。虽说从用户角度来说，www加不加通常没区别，但从技术上来说，www和非www根本不是一个域，换句话说，它们完全是两个网站；这两个网站可能由同一个人控制，也可能由不同的人控制。如果是后者，隐藏www就会出现问题。 一个实际的例子是，www.net.cn是万网的域名，然而它和net.cn完全无关——net.cn是中国版的n...

    通过例子与细节来通俗易懂理解聚类（K-Means）算法
    科学研究

    通过例子与细节来通俗易懂理解聚类（K-Means）算法

    江海志 6年前 (2018-09-10) 10913浏览 0评论

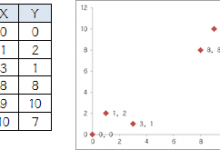
    聚类 今天说聚类，但是必须要先理解聚类和分类的区别，很多业务人员在日常分析时候不是很严谨，混为一谈，其实二者有本质的区别。 分类其实是从特定的数据中挖掘模式，作出判断的过程。比如Gmail邮箱里有垃圾邮件分类器，一开始的时候可能什么都不过滤，在日常使用过程中，我人工对于每一封邮件点选“垃圾”或“不是垃圾”，过一段时间，Gmail就体现出一定的智能，能够自动过滤掉一些垃圾邮件了。...

    macOS 10.13 本地快照（local snapshot）导致“系统”文件变大
    电子设备

    macOS 10.13 本地快照（local snapshot）导致“系统”文件变大

    江海志 6年前 (2018-09-09) 15219浏览 0评论

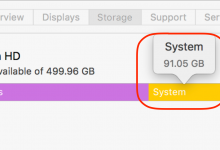
    升级到 macOS 10.13 后，大家可能发现“关于本机”中的存储那里，系统文件占用变大很多，有些甚至几天后发现能膨胀到几百GB。事实上这件事情在大概 El Captain 的时候就发生过。并不是 macOS High Sierra 系统膨胀的锅。  macOS HS 里 Time Machine 本地快照功能变成默认打开，并且不能关闭了，这些本地快照默认会保存24小时，这...

    科学研究

    计算机分领域顶级会议介绍

    江海志 6年前 (2018-09-04) 7289浏览 0评论

    比较权威的计算机会议排名就是CCF的那个排名，大家可以参考。 这里列出大家公认的计算机分领域著名会议（又名：顶级会议，顶会） Networking – SIGCOMM, NSDI, CoNEXT, MobiCom, MobiSys, WWW, INFOCOM Measurement – IMC, SIGMETRICS, Performance, IWQ...

    系统安全

    N-gram语言模型简单介绍与理解教程

    江海志 6年前 (2018-08-22) 3289浏览 0评论

    考虑一个语音识别系统，假设用户说了这么一句话：“I have a gun”，因为发音的相似，该语音识别系统发现如下几句话都是可能的候选：1、I have a gun. 2、I have a gull. 3、I have a gub. 那么问题来了，到底哪一个是正确答案呢？ 一般的解决方法是采用统计的方法。即比较上面的1、2和3这三句话哪一句在英语中出现的概率最高，哪句概率最高就...

    网络安全

    马尔可夫链蒙特卡洛(MCMC)采样详解

    江海志 6年前 (2018-07-03) 5520浏览 1评论

    这几天在看有关multimodal learning（多模态学习）的一些内容，随之就牵扯出了boltzman机，mcmc（马尔可夫链蒙特卡洛）采样等一系列内容。总之mcmc采样是ml领域非常重要的一个理论，此外，目前能找到的书籍或网络资源很多说的都不是很清楚。所以我决定为此专门写一篇博客。 要去讲清楚一个算法或一个模型，通常首先得明确两点，一是使用它的背景，二是更具针对性的该...

    网络安全

    马尔可夫链及吉布斯抽样(Markov Chain Monte Carlo and Gibbs Sampling)详解

    江海志 6年前 (2018-06-29) 5147浏览 0评论

    马尔可夫链及吉布斯抽样(Markov Chain Monte Carlo and Gibbs Sampling)详解 理解MCMC及一系列改进采样算法的关键在于对马尔科夫随机过程的理解。更多详尽的讨论请参见 重温马尔科夫随机过程。 对于给定的概率分布 ，我们希望能有便捷的方式生成它（）对应的样本。由于马氏链能收敛到平稳分布，于是一个很nice的想法（by Metropolis,...

    网络安全

    极大似然算法maximum likelihood 以及 EM算法详解

    江海志 7年前 (2018-06-25) 3437浏览 0评论

    机器学习十大算法之一：EM算法。能评得上十大之一，让人听起来觉得挺NB的。什么是NB啊，我们一般说某个人很NB，是因为他能解决一些别人解决不了的问题。神为什么是神，因为神能做很多人做不了的事。那么EM算法能解决什么问题呢？或者说EM算法是因为什么而来到这个世界上，还吸引了那么多世人的目光。 我希望自己能通俗地把它理解或者说明白，但是，EM这个问题感觉真的不太好用通俗的语言去说明...

    网络安全

    什么是P问题、NP问题，NPC问题和NP-hard问题

    江海志 7年前 (2018-06-19) 2972浏览 0评论

    这或许是众多OIer最大的误区之一。 你会经常看到网上出现“这怎么做，这不是NP问题吗”、“这个只有搜了，这已经被证明是NP问题了”之类的话。你要知道，大多数人此时所说的NP问题其实都是指的NPC问题。他们没有搞清楚NP问题和NPC问题的概念。NP问题并不是那种“只有搜才行”的问题，NPC问题才是。好，行了，基本上这个误解已经被澄清了。下面的内容都是在讲什么是P问题，什么是NP...

    汇编中的分支与循环
    编程开发

    汇编中的分支与循环

    江海志 7年前 (2018-04-03) 5003浏览 0评论

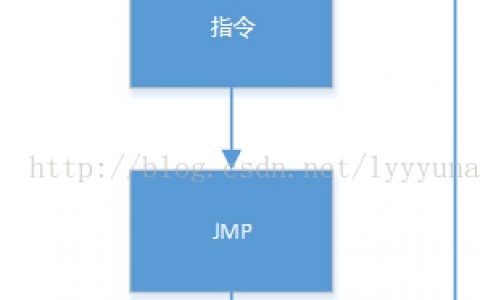
    在高级语言程序设计中，我们不仅要求程序能够顺序执行，还要求其能够执行不同分支，或者重复执行某些操作。在汇编语言中，同样具有相同的能力，可以由相应的指令来控制程序的执行流程。因为毕竟高级语言都是汇编实现的，只是不直观而已。 转移 无条件转移为JMP，类似c语言中的 goto。在c语言中，goto是不推荐使用的，会使程序难以控制和理解，但在汇编中，没有相应的if 和 while语句...

    编程开发

    什么是回调函数(callback function)，它有什么作用？

    江海志 7年前 (2018-04-02) 6229浏览 0评论

    编程分为两类：系统编程（system programming）和应用编程（application programming）。所谓系统编程，简单来说，就是编写库；而应用编程就是利用写好的各种库来编写具某种功用的程序，也就是应用。系统程序员会给自己写的库留下一些接口，即API（application programming interface，应用编程接口），以供应用程序员使用。...